PPO——近端策略优化算法

引言： 近端策略优化（PPO）是一种新的强化学习策略梯度方法，该方法通过与环境交互采样数据和使用随机梯度上升优化“替代”目标函数来交替进行。标准的策略梯度方法每个数据样本执行一次梯度更新，PPO提出了一种新的目标函数能够实现多轮小批量更新，它具备信任区域策略优化（TRPO）的部分优势，但实现起来更为简单、适用性更广，并且（从经验上看）具有更好的样本复杂度。实验结果表明PPO优于其他在线策略梯度方法，并且在样本复杂度、简便性和实际运行时间之间取得了良好的平衡。

✈️ PPO算法介绍

算法归类

PPO 是目前强化学习领域最主流的算法之一，它在分类谱系中占据着核心位置：

基于策略 (Policy-Based)：PPO 的核心是直接优化策略 π(a|s)，而不是像 DQN 那样间接优化价值 Q。
在线策略 (On-Policy)：PPO 是一种 On-Policy 算法。这意味着“采样的策略”和“学习的策略”必须是同一个。它不能像 DQN 那样使用经验回放池（Replay Buffer）里的过期数据，因此每次更新完策略后，旧的数据就必须丢弃。
演员-评论家框架 (Actor-Critic)：PPO 通常结合 Actor-Critic 架构。Actor 负责决策，Critic 负责打分（估计优势函数），两者相辅相成。

适用范围与局限

适用范围：
- 连续与离散动作空间：PPO 的最大优势之一是通用性。它既可以玩《超级马里奥》（离散动作），也可以控制机器人手臂抓取物体（连续动作）。
- 复杂环境：在许多高维、复杂的环境中（如 OpenAI Five 打 Dota2），PPO 表现出了极强的稳定性。
局限性：
- 样本效率较低：由于是 On-Policy 算法，数据用完即弃，相比于 Off-Policy 算法（如 SAC, TD3），PPO 需要更多的交互数据才能收敛。
- 探索能力受限：PPO 倾向于在已知的安全区域内优化，对于需要深度探索（稀疏奖励）的任务，可能容易陷入局部最优。

基本思想

PPO 的核心思想可以概括为：“步子迈小点，走得稳一点”。

在传统的策略梯度（Policy Gradient）中，如果学习率设置得太大，策略更新幅度过猛，很容易导致模型性能“断崖式下跌”，而且很难恢复。 TRPO（信任区域策略优化）试图通过复杂的数学约束（KL 散度）来限制更新幅度，但计算量太大。

PPO 继承了 TRPO 的思想，但用了一种更简单的工程方法（截断/Clipping）来实现：我们在目标函数里强行规定，新策略 π_new 和旧策略 π_old 的差异不能太大。如果差异太大，就不给奖励，甚至给惩罚。这保证了每一次更新都是在“信任区域”内的安全提升。

🚀 PPO算法流程

PPO 的强大来自于三个核心组件的有机结合：GAE 用于准确估计优势，KL 或 CLIP 用于限制更新幅度。

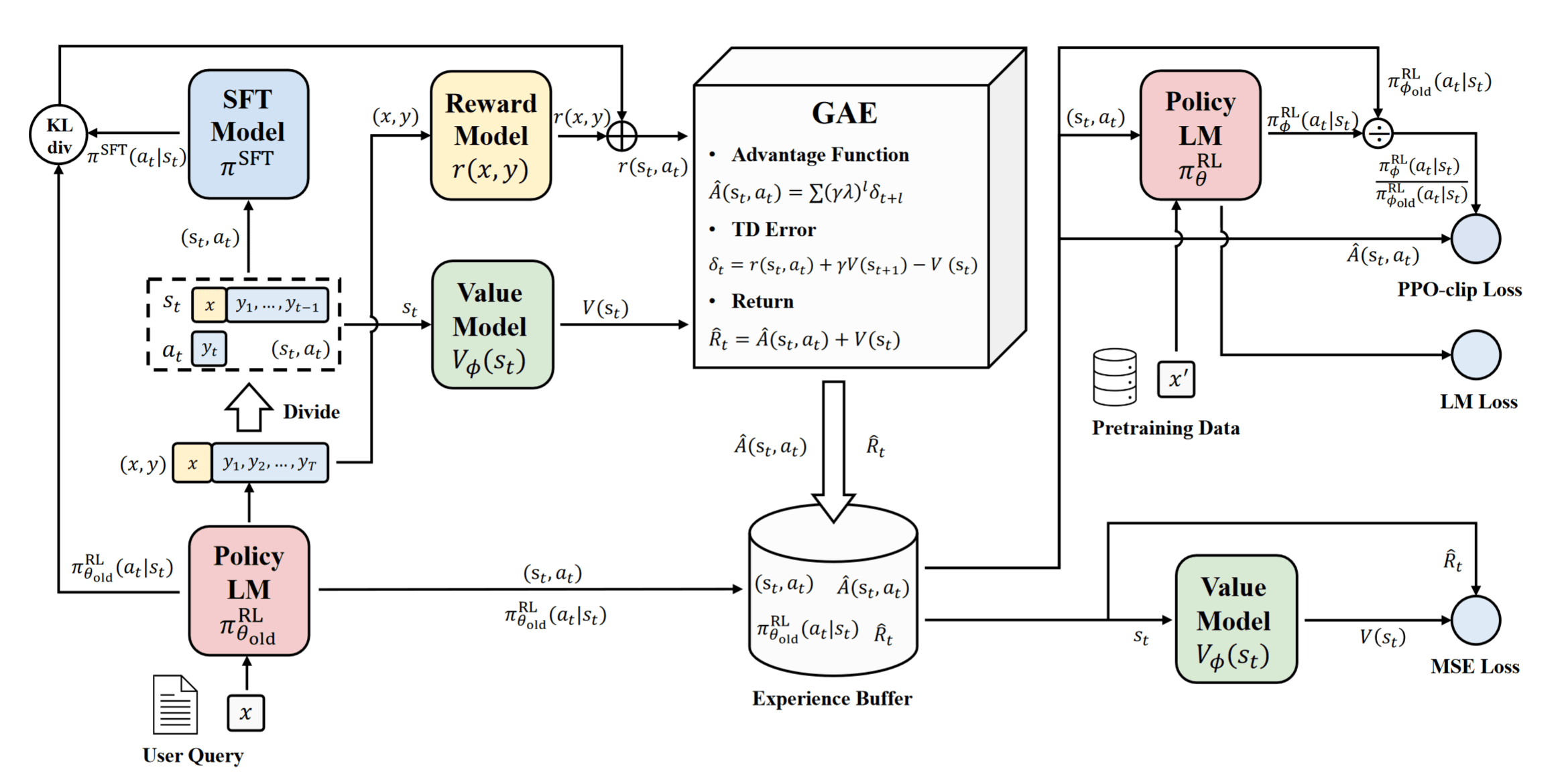
优势函数 GAE (Generalized Advantage Estimation)

在策略梯度中，我们需要评估一个动作“好不好”，这需要用到优势函数 (Advantage Function) A(s, a)。如果直接用蒙特卡洛回报 G_t 减去基线 V(s)，方差会很大；如果用 TD 差分，偏差会很大。

GAE 提出了一种在偏差和方差之间做权衡的方法。它定义了一个指数加权的优势估计：

$$ A_t^{GAE} = \sum_{l=0}^{\infty} (\gamma \lambda)^l \delta_{t+l} $$

其中 δ_t = r_t + γV(s_t + 1) − V(s_t) 是单步的 TD Error。

λ = 0：GAE 变成了普通的 TD Error（偏差大，方差小）。
λ = 1：GAE 变成了蒙特卡洛估计（偏差小，方差大）。
PPO 的选择：通常取 λ ≈ 0.95，在两者之间取得最佳平衡。

替代目标函数与概率比率 (Surrogate Objective)

为了能够利用旧策略 π_{θ_old} 采样的数据来更新当前的新策略 π_θ（即实现多轮小批量更新），PPO 引入了重要性采样 (Importance Sampling) 的技巧。

我们需要定义新旧策略在动作概率上的比率 (Probability Ratio)：

$$ r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)} $$

基于这个比率，我们可以构建一个最基础的替代目标函数（Conservative Policy Iteration, CPI）：

$$ L^{CPI}(\theta) = \mathbb{E}_t \left[ r_t(\theta) A_t \right] = \mathbb{E}_t \left[ \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)} A_t \right] $$

公式解析：

r_t(θ)：衡量了新策略相对于旧策略的变化幅度。
- 如果 r_t = 1，说明新旧策略一样。
- 如果 r_t > 1，说明新策略比旧策略更倾向于选择该动作。
优化逻辑：
- 当动作优势 A_t > 0（好动作）时，最大化目标函数会促使 r_t 变大，即增加该动作的概率。
- 当动作优势 A_t < 0（坏动作）时，最大化目标函数会促使 r_t 变小，即抑制该动作的概率。

存在的问题： 如果没有约束，直接最大化 L^CPI 会导致 r_t 发生剧烈变化（例如为了追求高分，把某个好动作的概率瞬间提得非常高）。这会导致新策略 π_θ 严重偏离旧策略，破坏训练的稳定性。因此，我们需要接下来的 CLIP 剪切 机制来限制它。

剪切 CLIP (PPO-Clip)

这是 PPO 的第二种变体，也是目前最流行、最常用的版本。它不需要计算复杂的 KL 散度，而是直接用 min 和 clip 函数来锁死更新幅度。

定义概率比率 $r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$。PPO-Clip 的目标函数为：

L^CLIP(θ) = 𝔼_t[min (r_t(θ)A_t, clip(r_t(θ), 1 − ϵ, 1 + ϵ)A_t)]

公式解析：

r_t(θ)A_t：这是原始的策略梯度目标。我们希望 A_t > 0 时 r_t 变大（增加好动作的概率）。
clip(..., 1 − ϵ, 1 + ϵ)：强制将比率限制在 [0.8, 1.2] 之间（假设 ϵ = 0.2）。
min 操作：这是一个悲观的下界估计。
- 当动作是好的 (A_t > 0)：如果模型概率提升太多（超过 1.2 倍），目标函数就被截断，不再给予奖励。这防止了“过度自信”。
- 当动作是坏的 (A_t < 0)：如果模型概率降低太多（低于 0.8 倍），目标函数也被截断。这防止了“过度恐慌”导致策略坍塌。

通过这种简单粗暴的“截断”机制，PPO 极其高效地实现了策略的平稳更新。

⚖️ 损失函数与优化目标

仅仅依靠 CLIP 剪切目标只能优化策略网络（Actor），但在 PPO 的实际应用中（通常采用 Actor-Critic 架构），我们需要构建一个复合的总目标函数 (Total Objective Function)，以便同时完成策略改进、价值函数拟合以及鼓励探索这三大任务。

PPO 的最终优化目标 L_t^Total(θ) 由三部分组成：

$$ L_t^{Total}(\theta) = \underbrace{L_t^{CLIP}(\theta)}_{\text{策略目标}} - \underbrace{c_1 L_t^{VF}(\theta)}_{\text{价值损失}} + \underbrace{c_2 S[\pi_\theta](s_t)}_{\text{熵正则化}} $$

我们通过最大化这个总目标函数来更新网络参数（或者通过最小化其负值）。

策略目标 (Policy Objective)

即前文提到的剪切目标 L_t^CLIP。这是核心部分，用于提升策略的表现，同时确保更新幅度在安全范围内。

价值函数损失 (Value Function Loss)

为了计算优势函数 A_t（用于指导策略更新），我们需要一个 Critic 网络来估计状态价值 V(s)。Critic 越准，优势估计就越准。因此，我们需要最小化价值网络的预测误差。通常使用均方误差 (MSE)：

L_t^VF(θ) = (V_θ(s_t) − V_t^target)²

V_θ(s_t)：当前网络预测的状态价值。
V_t^target：真实的价值目标（通常由计算出的回报 G_t 或 GAE 推算出的价值替代）。
c₁：价值损失系数（通常取 0.5），用于平衡策略优化和价值拟合的权重。
注：公式中的负号表示我们要最大化总目标，即等同于最小化价值误差。

PPO 的价值函数更新通常被视为一个回归问题。与 DQN 不同，PPO 由于是 On-Policy 算法，其价值目标是基于当次交互轨迹计算得出的固定回报（如 GAE），因此不需要使用额外的目标网络（Target Network）或软更新机制

熵正则化 (Entropy Bonus)

在强化学习中，过早收敛（Premature Convergence）是一个常见问题，即智能体在还没探索完环境时就认定某种次优策略是最好的，从而不再尝试其他可能。为了解决这个问题，我们在目标函数中加入策略熵 (Entropy) 项 S。熵越大，代表策略越随机（探索性越强）；熵越小，代表策略越确定。

S[π_θ](s_t) = −∑aπ_θ(a|s_t)log π_θ(a|s_t)