DPO——直接偏好优化算法

引言： 直接偏好优化算法（DPO）是一种新的参数化方式，能够以闭式解的形式提取相应的最优策略，使仅通过简单的分类损失就能解决标准的RLHF问题。它稳定、高效且计算量小，无需在微调过程中从语言模型中进行采样，也不需要进行大量的超参数调整。我们的实验表明，DPO能够对语言模型进行微调，使其与人类偏好保持一致，效果达到甚至优于现有方法。值得注意的是，使用DPO进行微调在控制生成内容的情感方面超过了基于PPO的RLHF，并且在摘要和单轮对话任务中，在响应质量上与之相当或有所提升，同时实现和训练过程也简单得多。

✈️ DPO算法介绍

算法归类

DPO（Direct Preference Optimization）在强化学习与大模型微调的版图中，属于一种返璞归真的算法：

离线策略 (Off-Policy / Offline)：严格来说，DPO 更接近于监督学习。它不需要在训练过程中让模型实时生成数据（像 PPO 那样采样），而是直接使用预先构建好的偏好数据集（Triplets: Prompt, Winner, Loser）。
基于策略 (Policy-Based)：它直接优化策略网络（LLM本身），没有显式的价值函数（Value Function）。
无奖励模型 (Reward-Free)：这是 DPO 最显著的标签。它不需要训练一个独立的 Reward Model，而是通过数学变换，将“奖励”隐式地包含在策略模型中。

适用范围与局限

适用范围：
- RLHF 替代方案：适用于所有需要人类偏好对齐的场景，如聊天机器人（Chatbot）、文本摘要、指令跟随等。
- 资源受限场景：由于不需要加载 Critic 和 Reward Model，DPO 的显存占用约为 PPO 的一半，非常适合在有限显存下微调大模型。
局限性：
- 数据分布偏移 (Out-of-Distribution)：DPO 属于离线学习，如果偏好数据集的分布与模型实际生成的分布差异过大，效果可能会打折扣。
- 缺乏探索 (Lack of Exploration)：PPO 在训练中会生成新数据进行探索，而 DPO 仅基于给定数据。对于需要极强逻辑推理或解空间很大的任务（如数学证明），DPO 可能不如在线 RL 方法（如 PPO 或 GRPO）。

基本思想

DPO 的核心洞察极其精妙：“奖励函数 r 和最优策略 π^* 是一体两面的。”

在 PPO 中，我们先训练一个奖励模型 r(x, y)，然后训练策略 π 去最大化这个 r。 DPO 的作者发现，对于一个特定的奖励函数，最优策略 π^* 的解析解是可以写出来的。既然如此，我们为什么不反过来，用策略 π 来表示奖励 r 呢？

这样，我们就可以把 RLHF 中那个“基于奖励模型的 Bradley-Terry 偏好概率”，直接转化为“基于策略概率的分类问题”。

🚀 DPO算法流程

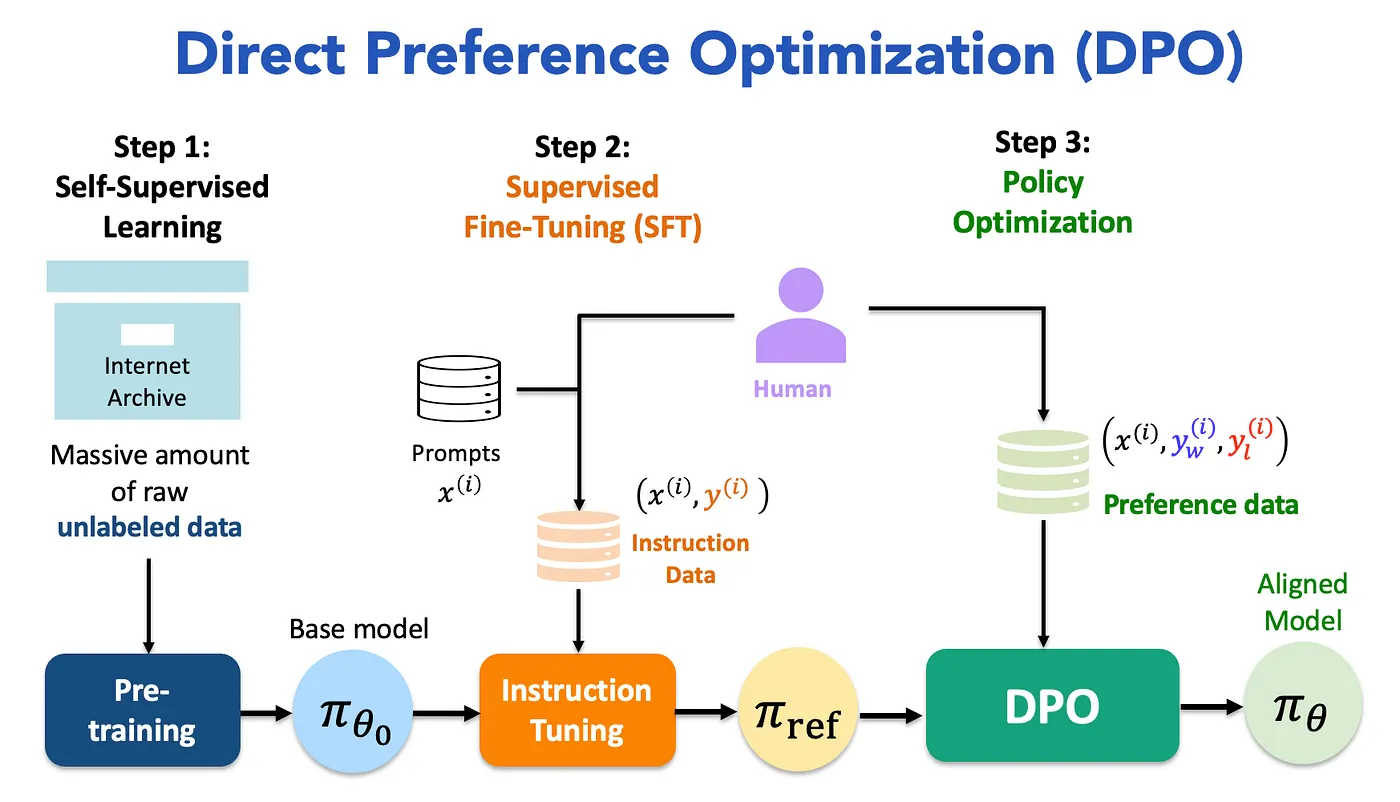
DPO 的核心优势在于将复杂的强化学习过程简化为直观的最大似然优化过程。它不再需要经验回放池（Replay Buffer）和复杂的采样（Sampling），而是直接在静态数据上进行计算。

DPO算法推导

这是 DPO 最核心的数学魔法。我们分三步走：

RLHF 的目标函数 标准的 RLHF 目标是最大化奖励，同时通过 KL 散度约束不偏离参考模型 π_ref： $$ \max_{\pi} \mathbb{E}_{x \sim D, y \sim \pi} [r(x,y) - \beta \log \frac{\pi(y|x)}{\pi_{ref}(y|x)}] $$

最优策略的解析解 通过变分法求解上述最优化问题，我们可以得到最优策略 π^* 的闭式解： $$ \pi^*(y|x) = \frac{1}{Z(x)} \pi_{ref}(y|x) \exp\left(\frac{r(x,y)}{\beta}\right) $$ 其中 Z(x) 是归一化因子。

反解奖励函数 (The Magic) 现在，我们对上面的公式进行移项，把奖励函数 r(x, y) 单独解出来： $$ r(x,y) = \beta \log \frac{\pi^*(y|x)}{\pi_{ref}(y|x)} + \beta \log Z(x) $$ 这个公式不仅消除了显式的奖励模型，还把奖励直接挂钩到了策略概率上！

代入 Bradley-Terry 模型 Bradley-Terry 模型定义了偏好概率： P(y_w > y_l) = σ(r(x, y_w) − r(x, y_l)) 我们将第三步反解出的 r(x, y) 代入上式（注意 Z(x) 会被消掉），最终得到了 DPO 的损失函数：

$$ L_{DPO}(\pi_\theta; \pi_{ref}) = - \mathbb{E}_{(x, y_w, y_l) \sim D} \left[ \log \sigma \left( \beta \log \frac{\pi_\theta(y_w|x)}{\pi_{ref}(y_w|x)} - \beta \log \frac{\pi_\theta(y_l|x)}{\pi_{ref}(y_l|x)} \right) \right] $$

DPO算法实现流程

DPO 的实际训练过程类似于监督学习（Supervised Learning），但需要同时维护两个模型进行前向传播。以下是单步更新的完整逻辑流程：

输入准备 (Input Preparation)
- 从偏好数据集 D 中采样一个批次的数据。
- 每条数据包含三部分：提示词 x (Prompt)，人类偏好的回答 y_w (Winner)，人类排斥的回答 y_l (Loser)。
参考模型前向传播 (Reference Forward)
- 使用参考模型（冻结参数，不更新）分别计算 y_w 和 y_l 的对数概率。
- 输出：log π_ref(y_w|x) 和 log π_ref(y_l|x)。
策略模型前向传播 (Policy Forward)
- 使用当前策略模型（需要更新参数）分别计算 y_w 和 y_l 的对数概率。
- 输出：log π_θ(y_w|x) 和 log π_θ(y_l|x)。
计算隐式奖励 (Implicit Reward Calculation)
- 计算两个模型对“胜出回答”的概率差值（Log Ratio）：R_w = β(log π_θ(y_w|x) − log π_ref(y_w|x))
- 计算两个模型对“落败回答”的概率差值（Log Ratio）：R_l = β(log π_θ(y_l|x) − log π_ref(y_l|x))
- 注：这里的 R_w 和 R_l 实际上代表了模型相对于参考模型获得的“隐式奖励”。
计算损失与反向传播 (Loss & Backward)
- 计算两者的奖励差值（Margin）：Margin = R_w − R_l。
- 将差值通过 Sigmoid 函数并取负对数，得到分类损失：Loss = −log σ(Margin)。
- 直观理解：我们希望 R_w 越大越好，R_l 越小越好，即拉大胜者和败者之间的距离。
- 根据 Loss 计算梯度，更新当前策略模型的参数 θ。

通过不断循环上述步骤，策略模型 π_θ 会逐渐“远离”参考模型对差答案的生成概率，并“靠近”参考模型对好答案的生成概率（同时加入人类偏好的修正）。

🔥 DPO的理论分析

LLM与奖励模型

在 PPO 时代，我们需要训练一个显式的 Reward Model (RM) 来充当“判卷老师”，告诉策略模型哪句话写得好。但 DPO 的数学推导揭示了一个深刻的理论事实：

语言模型本身就隐含了一个奖励模型。

冗余性：当我们训练 LLM 去逼近最优策略 π^* 时，策略模型的概率分布变化 $\frac{\pi(y|x)}{\pi_{ref}(y|x)}$ 其实就是在隐式地表达它对回复的偏好。
去中心化：因此，维护一个独立的 Reward Model 其实是冗余的，甚至可能因为 RM 自身的偏差引入额外的拟合误差。DPO 直接优化策略，相当于去掉了“中间商”，让偏好数据直接指导语言模型的生成概率。

Actor-Critic Algorithms 的不稳定性

为什么 PPO 这种 Actor-Critic 算法在大模型微调中如此难训？根本原因在于架构内部的复杂动态博弈：

移动的靶子 (Moving Target)：
- Actor 依赖 Critic 的打分来更新参数。
- Critic 依赖 Actor 采样的数据来更新参数。
- 只要其中一方稍微“跑偏”，另一方就会跟着学坏，导致训练震荡甚至崩塌。
复杂的超参数协调：
- PPO 需要同时维护 Actor、Critic、Reward Model、Reference Model 四个网络。
- 需要精细调节 GAE 系数 λ、截断系数 ϵ、价值损失系数 c₁、熵系数 c₂ 等，牵一发而动全身。