AlphaGomoku——MCTS算法与五子棋

引言： 蒙特卡洛搜索树（Monte Carlo Tree Search, MCTS）是一种用于决策的搜索算法，广泛应用于游戏、人工智能等领域。本文将介绍 MCTS 的基本原理，并通过一个五子棋的项目来展示如何使用 MCTS 算法进行游戏决策。

📖 蒙特卡洛搜索树（MCTS）

MCTS是什么？

MCTS是一种用于决策过程的启发式搜索算法，最早在2007年由Guillaume Chaslot在《Monte Carlo Tree Search: A New Framework for Game Backgammon》一文中提出。它通过模拟游戏过程来评估不同决策的优劣。MCTS的主要思想是通过反复模拟游戏过程，来估计每个决策的期望收益，从而选择最优决策。MCTS 算法通常由以下四个步骤组成：

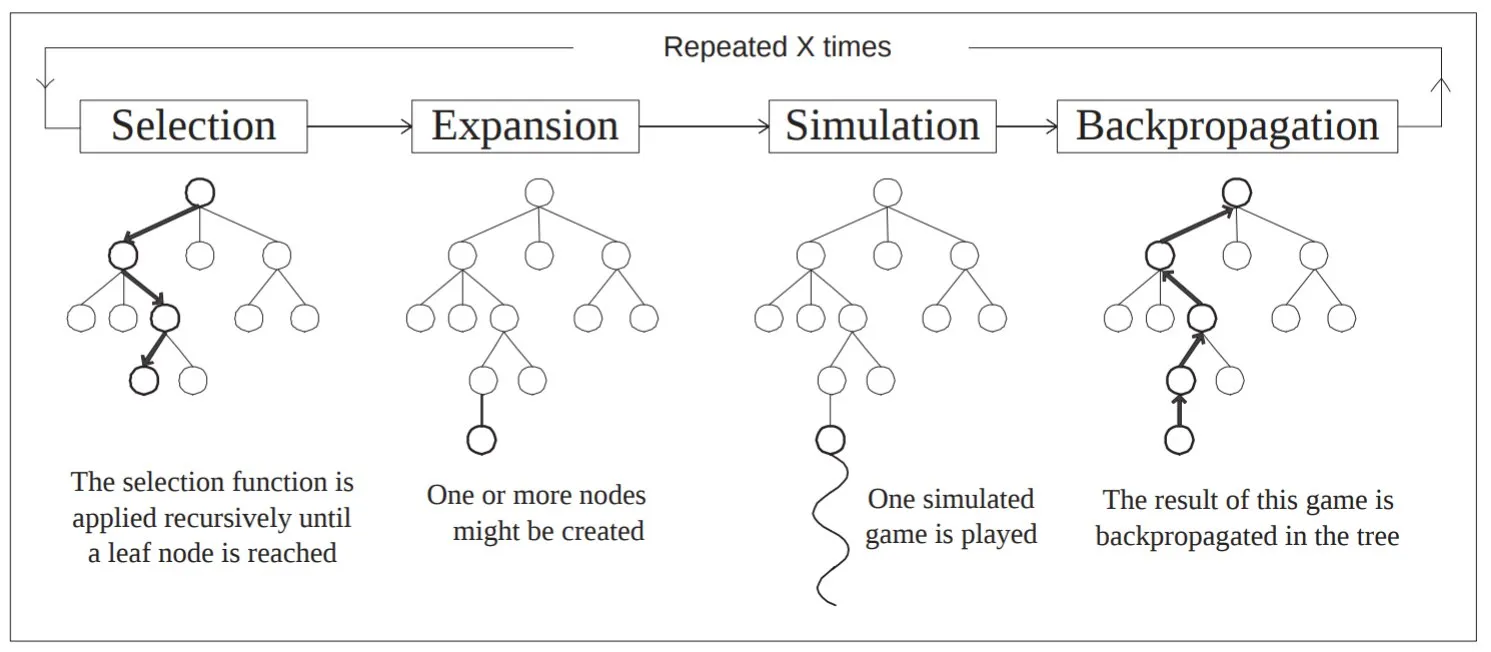
选择（Selection）：从当前树的根节点出发，沿着子节点逐层选择一个节点，直到到达一个未完全展开的节点或达到最大模拟深度为止。在这个过程中，选择最有可能导致最佳结果的节点，通常使用的是 UCB（上置信区间）策略。
扩展（Expansion）：如果所选节点不是终端节点，从该节点中随机选择一个未被访问过的子节点，添加到搜索树中。
模拟（Simulation）：从新扩展的节点开始，进行随机模拟（也称为“Playout”，通常使用随机策略），直到达到游戏的终局状态。根据终局状态的结果（如胜负或得分），评估该模拟。
反向传播（Backpropagation）：模拟结束后，将模拟结果（如胜负）回溯到树的每个节点。每个节点更新自己的统计数据，记录该节点的胜率或平均奖励。

🎯 如何理解MCTS？

我们以下五子棋为例，讲解MCTS算法的原理。

选择（Selection）

比如，当轮到我们下棋时，我们会在脑海中进行推演：我们下在A点，对手可能会下在B点，然后我们下在C点，对手可能会下在D点，以此类推。这个过程就是MCTS算法中的选择（Selection）过程。我们通过模拟不同的下棋路径，来选择一个最有利的下棋点。

这个过程的每一步选择都可以建模成一个多臂老虎机问题，即每次下棋都相当于选择一个老虎机臂，然后通过模拟来估计这个臂的收益。我们希望选择一个收益最大的臂，即选择一个最有利的下棋点。

那么，如何选择一个最有利的下棋点呢？我们可以使用上置信界（Upper Confidence Bound，UCB）算法，即选择一个收益最大的臂，同时考虑臂的探索程度。具体来说，UCB策略的计算公式为：

$$ UCB = \frac{w}{n} + c \sqrt{\frac{\ln N}{n}} $$

其中，w是臂的收益，n是臂被选择的次数，N是所有臂被选择的次数，c是一个常数，用于控制探索和利用的平衡。通过这个公式，我们可以选择一个收益最大的臂，同时考虑臂的探索程度。

探索（Exploration）和利用（Exploitation）是强化学习中的一个重要概念。

探索：基于已有知识选择奖励最大的动作。
利用：选择当前已知的最优动作，以获得最大的奖励。

有效的策略通常在探索与利用之间找到平衡。过度利用可能导致智能体停留在次优解，而过度探索则可能浪费资源。在MCTS算法中，通过UCB策略，可以在探索和利用之间找到平衡，从而选择一个最有利的下棋点。

扩展（Expansion）

比如，我们在脑海中推演到了一个新的局面：我们下在A点，对手应在了B点，此时棋盘出现了一个我们从未深入思考过的布局。我们需要决定下一步该往哪里探索，这个将新的可能性加入我们“推演地图”的过程，就是扩展（Expansion）。

在算法中，当“选择”过程走到了一个叶子节点（即还没有被完全推演过的节点），只要游戏未结束，我们就会创建一个或多个新的子节点（比如尝试下在C点或D点），并将这些新节点添加到我们的搜索树中。这相当于我们在脑海的棋谱中，新开辟了一条未知的路径，准备一探究竟。

模拟（Simulation）

既然我们要一探究竟，就需要知道这条新路径到底好不好。但是我们不可能穷尽之后的所有变化。于是，我们采用一种“快速推演”的方法：从这个新节点开始，在脑海中快速地推演（通常是随机地）棋局走向，直到分出胜负或平局。这个过程就是模拟（Simulation）。

这就像我们在脑海中按下了“快进键”，不再精细计算每一步，而是大致预估一下：“如果局面发展成这样，最后谁赢面大？”。虽然这种随机模拟单次看起来很粗糙，但只要模拟次数足够多，它就能有效地反映出该局面的优劣。

反向传播（Backpropagation）

当模拟结束后，我们得到了一个结果（比如我们输了），我们就会总结这个失败的经验，告诉自己下次避免走这个路径。这个过程就是反向传播（Backpropagation）。

在算法中，我们会沿着刚才选择的路径从叶子节点回到根节点，更新路径上每个节点的统计数据：

n（访问次数）：该节点参与推演的次数 +1。
w（累计收益）：如果模拟结果是我们赢了，则该节点的胜利分数增加。

通过不断地循环这四个步骤，我们的搜索树会越来越庞大，统计数据也越来越准确，最终指引我们下出最强的一步棋。

📰 MCTS的应用

MCTS与AlphaGo

AlphaGo 是由 Google DeepMind 开发的人工智能围棋程序，它的核心正是采用了 MCTS（蒙特卡洛树搜索）与深度神经网络（策略网络和价值网络）相结合 的架构。

2015年10月，AlphaGo 与三届欧洲围棋冠军樊麾进行了首场秘密对决。AlphaGo 以 5:0 的比分完胜，这是人工智能系统首次在无让子的情况下击败职业围棋选手。

2016年3月，AlphaGo 挑战曾获得18次世界冠军的围棋传奇人物李世石。这场比赛吸引了全球超过2亿人观看。最终，AlphaGo 以 4:1 的比分取得胜利。 AlphaGo 与李世石的围棋对决

MCTS与LLM

随着 GPT-4 等大语言模型的爆发，NLP 领域取得了惊人的进展。然而，LLM 在处理数学证明、复杂逻辑推理时，仍面临“一本正经胡说八道”（幻觉）的问题。为了解决这一问题，研究界开始尝试将 System 2（慢思考/逻辑推理） 引入 LLM，而 MCTS 正是实现这一目标的最佳框架之一。

MCTSr —— 提升数学推理能力

📄 论文：《Accessing GPT-4 level Mathematical Olympiad Solutions via Monte Carlo Tree Self-refine with LLaMa-3 8B》
🏛️ 机构：复旦大学、上海人工智能实验室等

在数学奥林匹克等高精度任务中，LLM 往往因为一步推理错误而导致全盘皆输。为了解决这个问题，研究团队提出了 MCT Self-Refine (MCTSr) 算法。

核心痛点：LLM 的生成是概率性的，容易产生幻觉，缺乏自我纠错机制。
解决方案：
- 将解题过程建模为 MCTS 的搜索树。
- 系统探索：利用 MCTS 探索不同的解题路径。
- 自我修正：结合 LLM 的自我反思能力（Self-Refine），对搜索过程中的节点进行评估和细化。
成果：该方法成功利用较小的模型（LLaMa-3 8B）实现了媲美 GPT-4 级别的数学解题能力。

🔗 阅读论文 (arXiv:2406.07394)

Marco-o1 —— 扩展开放式推理空间

📄 论文：《Marco-o1: Towards Open Reasoning Models for Open-Ended Solutions》
🏛️ 机构：阿里研究团队

受 OpenAI o1 模型卓越推理能力的启发，阿里团队开源了 Marco-o1 推理模型，旨在解决更复杂的现实世界挑战。

核心目标：探索 o1 类的推理模型能否推广到缺乏明确标准答案、且奖励难以量化的开放式问题领域。
解决方案 (Marco-o1-MCTS)：
- 扩展解空间：将 LLM 与 MCTS 结合，允许模型尝试多种推理路径。
- 置信度引导：利用模型输出的置信度作为信号，指导 MCTS 的搜索方向，从而在复杂的解空间中找到更优解。
意义：通过 MCTS 扩展了模型的思考维度，使其在 AIME 和 CodeForces 等平台上展现出超越传统模型的推理能力。

🔗 阅读论文 (arXiv:2411.14405)