DQN——Deep Q-Learning算法

引言： DQN（Deep Q-Network）是一种基于深度学习的强化学习算法，它通过构建一个神经网络来估计状态-动作值函数（Q函数），从而实现智能体的决策过程。DQN算法的核心思想是通过不断与环境交互，学习到最优的Q函数，从而找到最优的策略。本文将介绍DQN算法的基本原理、实现方法。

✈️ DQN算法介绍

算法归类

从分类体系上看，DQN 完美继承了 Q-Learning 的基因，同时引入了深度学习的特性：

基于价值 (Value-based)：DQN 不直接输出动作的概率，而是输出每个动作的价值（Q值），通过 arg max Q 来选择动作。
无模型 (Model-free)：智能体不需要理解环境的物理规律（如重力、摩擦力），直接通过试错来学习。
离轨策略 (Off-policy)：DQN 使用经验回放池（Experience Replay），这意味着它学习的数据来自于“过去的自己”甚至“随机策略”，而不是当前的策略。
深度强化学习 (Deep RL)：这是它与 Q-Learning 最大的区别，使用神经网络（Function Approximator）来代替表格。

适用范围与局限

适用范围：
- 高维状态空间：这是 DQN 的杀手锏。它可以直接处理图像（像素矩阵）、复杂的传感器数据，解决了表格型方法无法处理“无限状态”的问题。
- 离散动作空间：适用于像《王者荣耀》放技能、Atari 游戏（上下左右）这类动作有限的任务。
局限性：
- 难以处理连续动作：对于机器人关节控制（角度是连续小数）这类任务，DQN 需要将动作离散化，但这会导致动作维度爆炸。通常需要借助 Actor-Critic 类算法（如 DDPG）来解决。
- 训练不稳定：相比于简单的查表，神经网络的收敛极其敏感，对超参数（学习率、Replay Buffer 大小等）要求很高。

基本思想

在 Q-Learning 中，我们有一个真实的表格 Q_table(s, a)。在 DQN 中，我们抛弃表格，用一个神经网络 Q(s, a; θ) 来拟合这个价值函数。

输入：状态 s（例如一张 84 × 84 的游戏截图）。
经过：卷积层 (CNN) 提取特征 → 全连接层 (FC) 进行推理。
输出：所有可能动作的 Q 值向量。例如 [Q(s, 左), Q(s, 右), Q(s, 跳)]。

我们的目标是训练参数 θ，使得网络预测的 Q 值逼近真实的期望回报。

🚀 DQN算法流程

DQN 之所以能成功，是因为它引入了两个关键机制来解决神经网络训练不稳定的问题：经验回放和目标网络。

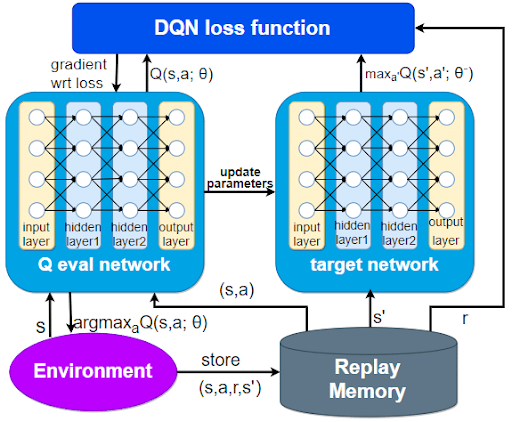
经验回放 (Experience Replay)

问题：在玩游戏时，时间是连续的。这一秒的状态 s_t 和下一秒的状态 s_t + 1 非常相似。如果直接把这些高度相关的数据喂给神经网络，网络会“钻牛角尖”（过拟合），导致训练发散。

解决方案：建立一个记忆库 (Replay Buffer)。

存储：智能体与环境交互，把每一步产生的数据 (s, a, r, s^′) 存入一个容量有限（例如 100万）的队列中。
采样：在训练时，不按顺序学习，而是从记忆库中随机抽取 (Random Batch) 一批数据（例如 32 条）来进行梯度下降。

作用：

打乱相关性：随机采样消除了数据之间的时间相关性，满足了神经网络训练所需的独立同分布 (I.I.D) 假设。
数据复用：一条经验可以被多次抽取和学习，提高了数据利用率。

目标网络 (Target Network)

问题：在 Q-Learning 的更新公式中，目标值 Target = r + γmax Q(s^′)。在 DQN 中，如果只用一个网络，那么 Q(s)（当前估计）和 Q(s^′)（目标估计）都由同一个网络参数 θ 决定。这就像“左脚踩右脚上天”——每次更新参数 θ，不仅预测值变了，目标值也变了。目标忽高忽低，导致网络很难收敛。

解决方案：使用两个结构相同但参数独立的网络。

当前网络 (Eval Net, 参数 θ)：负责选择动作，并利用梯度下降实时更新参数。这是我们需要训练的“主网络”。
目标网络 (Target Net, 参数 θ⁻)：专门负责计算目标 Q 值。它的参数不会实时更新，而是每隔一定步数（例如 C=1000 步）才从当前网络复制一次。

作用：通过“固定”目标网络一段时间，相当于给训练提供了一个暂时静止的靶子，极大地提高了训练的稳定性。

目标网络梯度更新

DQN 的训练本质上是一个回归问题 (Regression)。我们要最小化“当前网络的预测值”和“目标网络计算的真实值”之间的差距。

计算目标值 (TD Target) 对于采样出来的每一条数据 (s, a, r, s^′)，利用目标网络计算标签：

y = r + γmax_a^′Q(s^′, a^′; θ⁻)

注意这里使用的是 θ⁻（目标网络的旧参数）。

计算预测值 (Current Prediction) 利用当前网络计算当前状态动作的价值：

ŷ = Q(s, a; θ)

注意这里使用的是 θ（当前网络的最新参数）。

损失函数 (Loss Function) 使用均方误差 (MSE) 来衡量两者的差距：

L(θ) = 𝔼[(y − ŷ)²] = 𝔼[(r + γmax_a^′Q(s^′, a^′; θ⁻) − Q(s, a; θ))²]

梯度反向传播 对损失函数 L(θ) 关于 θ 求导，并使用 SGD 或 Adam 优化器更新当前网络的参数：

θ ← θ − α∇_θL(θ)

通过不断的迭代，当前网络 Q 会越来越精准，最终学会最优策略。

🤔 Think Different

我们经常看到一个有趣的现象：在不同领域、不同时间被发明的算法，其核心数学原理竟然惊人地一致。

DQN 中生硬的硬更新（Hard Update），在后来的 DDPG 算法中演化为了丝滑的软更新（Soft Update），而这一思想后来竟成为了无监督学习（如 MoCo）的基石。这证明了通过平滑目标来稳定训练是一个通用的、解决共性问题的方法论。

目标函数的更新方法

DQN (2015) 为了稳定训练，使用了 Hard Update：

机制：目标网络 θ⁻ 平时完全不动，每隔 C 步（比如 1000 步），直接把当前网络 θ 的参数完全复制过去。
缺点：目标值 y 会呈现“阶梯状”跳变。在复制参数的那一瞬间，目标值突然大幅变化，可能导致 Loss 瞬间飙升，训练过程产生剧烈震荡。

DDPG (2016) 为了处理连续动作空间，对稳定性要求更高，因此引入了 Soft Update：

机制：目标网络每一步都更新，但每次只更新一点点。
公式： θ⁻ ← τθ + (1 − τ)θ⁻ 其中 τ 是一个极小的系数（例如 τ = 0.001）。
效果：这意味着目标网络 θ⁻ 是当前网络 θ 的指数移动平均 (Exponential Moving Average, EMA)。目标值的变化不再是剧烈的跳变，而是像“斜坡”一样平滑过渡。

无监督学习中的“软更新”

当我们把 DDPG 的软更新公式，和几年后计算机视觉领域 MoCo (Momentum Contrast) 的更新公式放在一起时，会发现它们完全是一回事：

算法	领域	术语	公式 (m = 1 − τ)	目的
DDPG	强化学习 (RL)	Soft Update	θ⁻ ← τθ + (1 − τ)θ⁻	稳定 TD Target，防止策略震荡
MoCo	自监督学习 (SSL)	Momentum Update	θ_k ← mθ_k + (1 − m)θ_q	维持队列特征一致性，防止特征剧变

DDPG 的 τ ≈ 0.001 对应了 MoCo 的 m ≈ 0.999。
它们都在做同一件事：制造一个“沉稳的老师”。
- 即使“学生”（当前网络/Query Encoder）因为学习率高、Batch 噪声大而上蹿下跳；
- “老师”（目标网络/Key Encoder）依然保持淡定，只吸收学生长期的平均趋势，过滤掉高频的噪声。

为什么好的方法是通用的？

为什么这种参数的凸组合（Convex Combination）能解决共性问题？本质上有三个原因：

低通滤波 (Low-Pass Filtering)：深度学习的训练过程充满了随机噪声（SGD 的随机性、环境采样的随机性）。软更新本质上是一个低通滤波器。它过滤掉了参数更新中的高频震荡（Noise），只保留了参数演化的低频趋势（Trend）。无论是 RL 还是 SSL，只要存在非平稳性，这种滤波都是必须的。
滞后带来稳定 (Lag implies Stability)：控制理论告诉我们，在一个闭环反馈系统（Self-Loop）中，如果反馈过于灵敏，系统容易发散（啸叫）。通过软更新引入滞后 (Lag)，相当于增加了系统的阻尼，虽然减慢了响应速度，但极大地提高了系统的鲁棒性。
平滑流形 (Smooth Manifold)：在 DDPG 面对的连续控制和 MoCo 面对的高维特征空间中，参数的微小跳变可能导致输出结果在流形上发生巨大位移。软更新保证了目标函数在优化表面上的轨迹是连续且平滑的，这对于基于梯度的优化器来说是最友好的环境。

从 DQN 的Hard Update，到 DDPG 的Soft Update，再到 MoCo 的Momentum Update，看到了：