Q-Learning——一种基于值迭代的强化学习算法

引言： Q-Learning是一种基于值迭代的强化学习算法，它通过不断更新Q值来优化策略。Q值表示在给定状态下采取某个动作的预期回报。Q-Learning算法通过最大化Q值来选择最优动作，从而实现最优策略的求解,下面有是Q-Learning算法介绍与井字棋游戏的实现。

✈️ Q-Learning算法介绍

算法归类

从分类上来看，Q-Learning 具有以下标签：

基于价值 (Value-based)：输出动作的价值，而非直接输出动作概率。
离轨策略 (Off-policy)：学习时使用的策略（目标策略，通常是贪婪的）与采集数据时的策略（行为策略，通常是 ϵ-greedy）不同。
无模型 (Model-free)：不需要知道环境的状态转移概率 P(s^′|s, a)。
在线 (Online)：通常是在与环境交互的过程中实时学习（尽管也可以结合经验回放）。

适用范围与局限

适用场景：适用于连续或离散、有限或无限状态空间、确定性或随机性的环境。
局限性：在处理高维状态空间（如图像输入）和连续动作空间（如机器人关节角度）时，传统的表格型 Q-Learning 表现不佳（因为表格存不下，通常需要升级为 Deep Q-Network）。

基本思想

Q-Learning 的核心是不需要知道环境的动态模型。智能体通过与环境的直接交互来学习策略。

核心机制：通过更新状态-动作值函数（Q值），来评估每个动作在每个状态下的价值。
更新方式：采用离线更新（Off-policy）方法，在每次交互后利用 Bellman 方程立即更新 Q 值，使得算法在训练过程中不断优化。
收敛目标：该过程持续进行，直到 Q 值函数收敛，最终得到最优策略 π^*。

🚀 Q-Learning算法流程

Q-Learning 是一种无模型的强化学习技术。在经典的表格型 Q-Learning 中，我们通常使用两个主要的矩阵（表格）来表示和更新信息。

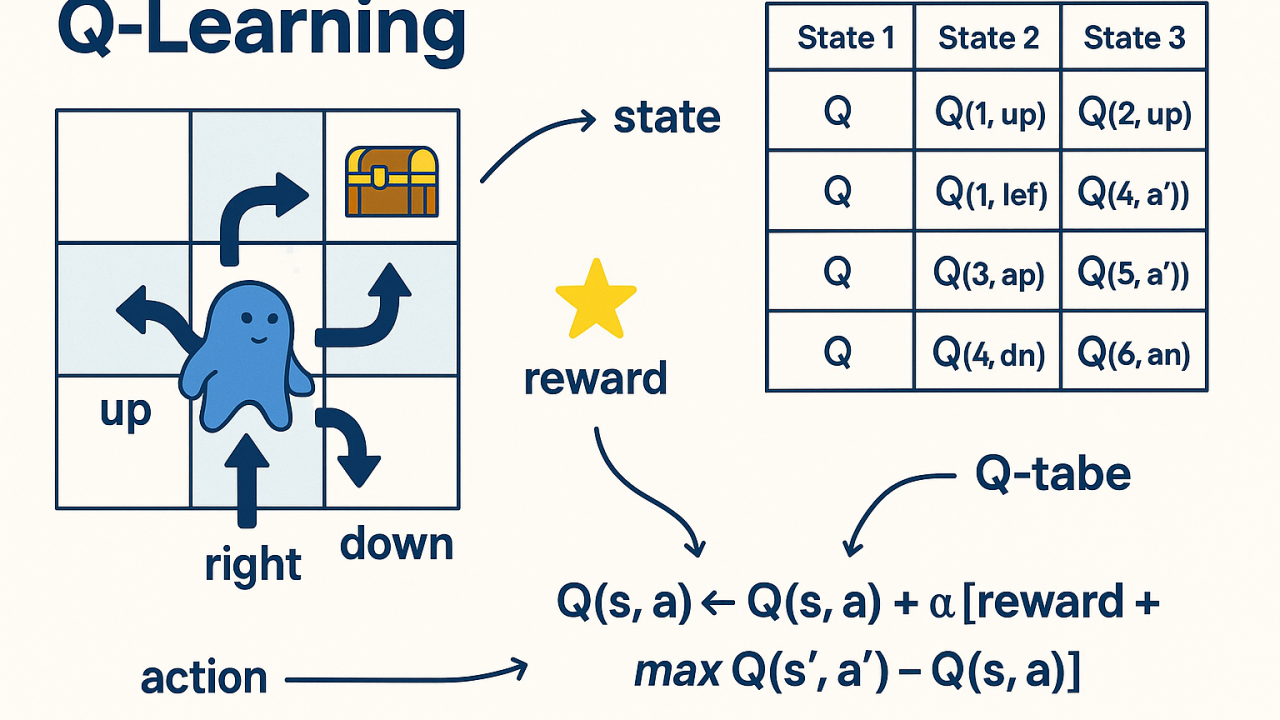
两个核心矩阵

奖励矩阵 (R-Table)

结构：每一行代表一个状态 (s)，每一列代表一个动作 (a)。
含义：矩阵中的元素 R(s, a) 表示在状态 s 下采取动作 a 时，从环境获得的即时奖励 (Immediate Reward)。
数值：可以是正数（奖励）、负数（惩罚）或零。

Q值矩阵 (Q-Table)

结构：同样每一行代表一个状态，每一列代表一个动作。
含义：矩阵中的元素 Q(s, a) 表示在状态 s 下采取动作 a，并在未来遵循最佳策略所能获得的预期累积回报。
关系：R 是环境给的反馈，Q 是智能体学到的经验。

算法核心步骤

Q-Learning 的核心思想是通过不断更新 Q 值来逼近最优 Q 函数 Q^*。

第一步：初始化

由于刚开始 Agent 对外界一无所知，矩阵 Q 通常初始化为零矩阵，如果状态数目未知，可以让 Q 从空表出发，每次发现新状态时动态增加行列。

第二步：状态转移与更新

Agent 在每一个 回合 (Episode) 中不断探索，直到到达目标状态。在每一步 (s → s^′ ) 中，遵循以下规则更新：

$$ Q(s, a) \leftarrow Q(s, a) + \alpha \left[ \underbrace{R(s, a) + \gamma \cdot \max_{a'} Q(s', a')}_{\text{现实 (Target)}} - \underbrace{Q(s, a)}_{\text{预期 (Prediction)}} \right] $$

公式参数详解：

s, a：当前的状态和采取的行为。
s^′, a^′：转移到的下一个状态及下一个行为。
γ (折扣因子, Discount Factor)：0 ≤ γ < 1。
- γ ≈ 0：智能体“短视”，只看重眼前的即时奖励。
- γ ≈ 1：智能体“远视”，更看重未来的长期奖励。
α (学习率, Learning Rate)：控制更新的步长（通常在 0 到 1 之间）。

第三步：循环与收敛

Episode（回合）：Agent 从任意初始状态出发，不断探索直到达到目标状态（或达到步数限制），这被称为一个 Episode。
无监督学习：在没有老师直接指导的情况下，Agent 通过“尝试-反馈-更新”的循环，不断修正 Q 表中的数值。

随着 Episode 的增加，Q 表中的数值会越来越准确，最终 Agent 只需在每个状态 s 选择 Q(s, a) 最大的那个动作，就是最优策略。

📖 Q-Learning 求解

Q-Learning 的数学核心在于利用贝尔曼方程（Bellman Equation）进行迭代更新，逐步逼近最优的动作价值函数。

贝尔曼方程

贝尔曼方程是动态规划中的核心原理，它将一个状态的价值分解为即时奖励和折扣后的未来价值的总和。

对于状态价值函数 V_π(s) 和动作价值函数 Q_π(s, a)，贝尔曼期望方程表示为：

V_π(s) = ∑_a ∈ Aπ(a|s)[R(s, a) + γ∑_{s^′ ∈ S}P(s^′|s, a)V_π(s^′)]

Q_π(s, a) = R(s, a) + γ∑_{s^′ ∈ S}P(s^′|s, a)V_π(s^′)

符号定义：

S：状态空间。
A：动作空间。
π(a|s)：策略函数，表示在状态 s 下采取动作 a 的概率。
R(s, a)：在状态 s 下采取动作 a 获得的即时奖励（期望值）。
P(s^′|s, a)：状态转移概率，即从状态 s 采取动作 a 转移到状态 s^′ 的概率。
γ：折扣因子，0 ≤ γ < 1，用于平衡当前奖励与远期奖励。

Q-Learning 更新规则

Q-Learning 是一种无模型（Model-Free）算法，它不需要知道转移概率 P。它利用时间差分（Temporal Difference, TD）方法，直接通过经验数据来更新 Q 值。

其迭代更新规则如下：

$$ Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ \underbrace{R_{t+1} + \gamma \max_{a} Q(s_{t+1}, a)}_{\text{TD 目标 (Target)}} - \underbrace{Q(s_t, a_t)}_{\text{当前估计}} \right] $$

参数说明：

Q(s_t, a_t)：时间 t 下，状态 s_t 和动作 a_t 的估计价值。
R_t + 1：执行动作 a_t 后实际获得的即时奖励。
max_aQ(s_t + 1, a)：在下一状态 s_t + 1 中，假设采取最优动作所能获得的最大 Q 值（贪婪估计）。
α：学习率（Learning Rate），0 ≤ α ≤ 1，控制新旧信息的覆盖程度。
γ：折扣因子。

从贝尔曼方程到 Q-Learning

Q-Learning 算法的最终目标是找到一个最优策略 π^*，使得在该策略下每个状态动作对的 Q 值最大化，即：

π^* = arg max_πQ_π(s, a)

我们可以从贝尔曼方程推导出 Q-Learning 逼近的目标形式。

假设我们有一个策略 π，其对应的动作价值函数为 Q_π。根据贝尔曼方程：

Q_π(s, a) = R(s, a) + γ∑_{s^′ ∈ S}P(s^′|s, a)V_π(s^′)

由于最优状态价值 V^*(s^′) 等于在该状态下选择最优动作的 Q 值，即 V^*(s^′) = max_a^′Q^*(s^′, a^′)，我们可以进行替换。

如果我们将策略 π 设定为最优策略 π^*，则得到了贝尔曼最优方程（Bellman Optimality Equation）：

Q^*(s, a) = R(s, a) + γ∑_{s^′ ∈ S}P(s^′|s, a)max_a^′Q^*(s^′, a^′)

推导结论： 这个方程表明，最优动作价值 Q^*(s, a) 由即时奖励和下一状态所有可能动作中的最大 Q 值的期望构成。 Q-Learning 算法正是通过不断的采样和更新，利用 R + γmax Q(s^′, a^′) 来逼近上述方程中的期望值，从而在不知道 P(s^′|s, a) 的情况下求得马尔科夫决策过程的最优解。