GSPO——序列级策略优化算法

引言： 该研究提出 GSPO（Group Sequence Policy Optimization）算法，通过将优化粒度从 token 级别提升到 sequence 级别，解决了 GRPO 中「目标函数设计缺陷」「梯度噪声累积」「MoE 训练不稳定」等根本性问题。GSPO 已成功应用于 Qwen3 模型训练，在相同计算量下实现更好的性能和稳定性，且无需 Routing Replay 等复杂技巧即可稳定训练 MoE 模型。

✈️ GSPO 算法介绍

GRPO（Group Relative Policy Optimization）通过组内相对优势估计消除了对价值模型的依赖，成为大模型 RL 训练的主流方法之一。然而，作者在深入分析 GRPO 的目标函数后，发现其存在一个根本性的设计缺陷：GRPO 在 token 级别应用重要性权重，但这违反了重要性采样的基本原理。

重要性采样要求在多个样本上进行平均以纠正分布偏差，但 token 级别的权重基于单个样本，无法有效实现这一目的。这导致了高方差梯度噪声，在长序列上不断累积，最终可能导致模型崩溃。问题的核心在于：奖励是在序列级别给出的，而 GRPO 却在 token 级别进行优化，优化单位与奖励单位不匹配。

为此，作者提出了 GSPO（Group Sequence Policy Optimization）算法，核心改进是将优化粒度从 token 级别提升到 sequence 级别。GSPO 引入序列级重要性权重和序列级 Clipping，使优化单位与奖励单位对齐，从根本上解决了 GRPO 的理论缺陷。此外，GSPO 对 MoE 模型具有天然的稳定性支持，无需 Routing Replay 等复杂技巧。

🚀 GSPO 算法流程

GSPO 的目标函数定义如下：对于每个输入 x，采样一组输出 {y_i}_i = 1^G，然后优化：

其中 s_i(θ) 是序列级重要性权重，Â_i 是组级优势估计。与 GRPO 的关键区别在于：GSPO 在序列级别而非 token 级别应用重要性权重和 Clipping，使得优化单位与奖励单位保持一致。

序列级重要性权重

GRPO 为每个 token 计算独立的重要性权重，这些权重在序列中累积，导致方差不断增大。更严重的是，这种 token 级权重无法正确实现重要性采样的分布修正功能。

GSPO 引入序列级重要性权重：

该定义包含两个关键设计。首先，使用序列的整体 likelihood 比率而非单个 token 的比率，使权重反映的是整个响应的分布变化。其次，引入长度归一化（指数），将不同长度响应的重要性比率控制在统一的数值范围内，减少方差并防止少数 token 的 likelihood 变化导致序列级比率的剧烈波动。

序列级 Clipping

GSPO 将 Clipping 也提升到序列级别，直接对 s_i(θ) 进行裁剪，而非对每个 token 的 w_i, t(θ) 分别裁剪。一个显著的差异是 Clipping 范围：GRPO 通常使用 0.2-0.27 的范围，而 GSPO 使用 3e-4 到 4e-4，相差近两个数量级。

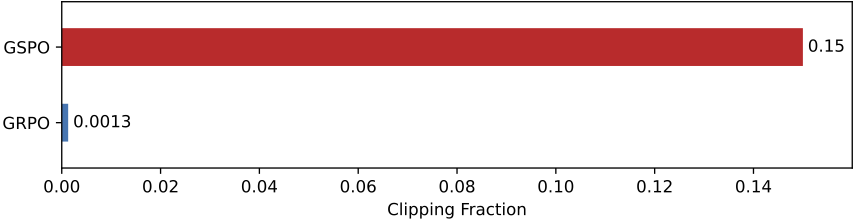
实验中观察到一个反直觉的现象：GSPO 裁剪的 token 比例远大于 GRPO，意味着使用更少的 token 进行梯度估计，但训练效率反而更高。这说明 GRPO 的 token 级梯度估计本质上充满噪声且低效，而 GSPO 的序列级方法提供了更可靠和有效的学习信号。

梯度分析对比

从梯度角度分析两种方法的本质差异。GSPO 的梯度（省略 Clipping）为：

与 GRPO 梯度的根本区别在于 token 的加权方式。在 GRPO 中，每个 token 有不同的重要性权重，这些权重在 (0, 1 + ε] 或 [1 − ε, +∞) 之间变化，累积后带来不可预测的后果。而在 GSPO 中，所有 token 共享相同的序列级权重 s_i(θ)，消除了 token 间权重不均匀带来的不稳定因素。

组级优势估计 Â_i 的定义与 GRPO 相同：

MoE 训练支持

GRPO 在训练 MoE（Mixture-of-Experts）模型时面临严重的路由波动问题：同一响应在梯度更新后激活的 experts 会显著变化，在 48 层模型中约有 10% 的路由发生改变。这导致 token 级重要性比率剧烈波动，训练极不稳定。

为解决这一问题，GRPO 需要采用 Routing Replay 技巧：缓存旧 policy 的激活 experts，在新 policy 中「重放」这些路由模式，人为约束路由的一致性。这不仅增加了实现复杂度，还限制了模型充分利用 MoE 的容量。

GSPO 天然解决了这一问题。由于采用序列级重要性权重，单个 token 的 likelihood 波动对整体比率的影响被大幅削弱。虽然个别 token 因路由变化可能产生较大的 likelihood 变化，但语言建模能力整体保持稳定，序列级 likelihood 不会剧烈波动。因此，GSPO 完全消除了对 Routing Replay 的依赖，允许模型充分利用 MoE 容量而无需人工约束。

🎯 训练细节与实验结果

作者以 Qwen3-30B-A3B-Base 冷启动微调模型为基础进行实验，评估基准包括 AIME’24（平均 Pass@1，32 次采样）、LiveCodeBench（2024.10-2025.02，平均 Pass@1，8 次采样）和 CodeForces（Elo 评级）。训练采用 off-policy 设置，每批 rollout 数据分成 4 个 mini-batch 进行梯度更新。GSPO 的 Clipping 范围设为左 3e-4、右 4e-4，而 GRPO 经过仔细调整后使用 0.2-0.27 的范围以保证公平对比。

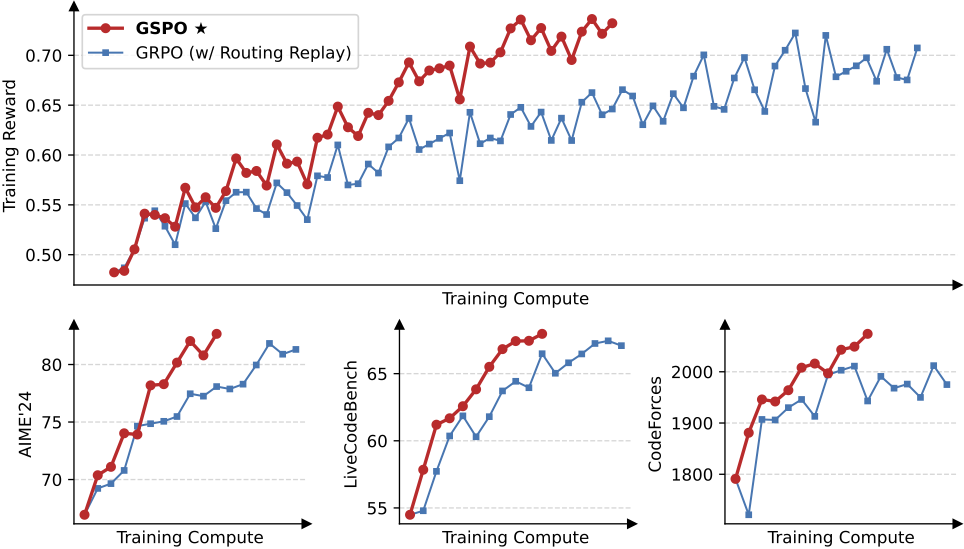基于Qwen3-30B-A3B-Base微调的冷启动模型的训练曲线。GSPO的训练效率显著高于GRPO 实验结果表明，GSPO 全程训练稳定，而 GRPO 存在不稳定问题。在相同训练计算量和查询消耗下，GSPO 实现了更好的训练精度和基准性能。更重要的是，GSPO 能够通过增加训练计算、更新查询集和延长生成长度实现持续的性能改进，已成功应用于 Qwen3 最新模型的 RL 训练。

GSPO 还带来了基础设施层面的优势。由于序列级 likelihood 比 token 级更能容忍精度差异，可以直接使用 inference engine（如 SGLang、vLLM）返回的 likelihood，无需 training engine 重新计算。这对 partial rollout 和 multi-turn RL 场景特别有利，支持 training-inference 分离的框架设计。

💡 洞察与结论

理论贡献方面，GSPO 的核心洞察是「优化单位应与奖励单位匹配」。GRPO 在 token 级别应用重要性权重违反了重要性采样的基本原理，而 GSPO 通过提升到序列级别，使目标函数在理论上更加合理。这一改进看似简单，却从根本上解决了长期困扰 LLM RL 训练的稳定性问题。

实践意义方面，GSPO 对 MoE 模型的原生支持具有重要价值。随着 MoE 架构在大模型中的广泛应用，一个无需额外技巧就能稳定训练 MoE 的 RL 算法将大幅降低工程复杂度。此外，对 inference engine likelihood 的容忍性简化了 RL 基础设施，使 training-inference 分离成为可能。

工业验证方面，GSPO 已成功集成到 Qwen3 的训练流程中，证明了其在工业级大规模训练中的有效性。从 GRPO 到 GSPO 的演进表明，在 LLM RL 领域，回归基础原理、确保理论正确性往往比复杂的工程技巧更为关键。

Notes > Reinforcement Learning

#Research #Algorithm #GSPO