GDPO——分组奖励解耦归一化策略优化算法
引言: GDPO(Group reward-Decoupled Normalization Policy Optimization)是一种针对多奖励强化学习优化的新方法。它解决了 GRPO(Group Relative Policy Optimization)在处理多奖励时存在的奖励信号压缩问题,通过对每个奖励进行独立的分组归一化,保留了不同奖励组合之间的细微差异,从而实现更准确的多奖励优化和显著提升的训练稳定性。
✈️ GDPO 算法介绍
研究背景
随着语言模型能力的不断增强,用户期望模型在提供准确响应的同时,还能在各种场景下符合多样化的人类偏好。为了实现这一点,强化学习(RL) pipeline 开始集成多个奖励,每个奖励捕获不同的偏好,以引导模型实现这些期望的行为。
目前,GRPO 是广泛使用的强化学习算法,但它主要用于优化单一目标奖励(通常是准确性)。当直接将 GRPO 应用于多奖励设置时,会将所有奖励相加后进行统一的分组归一化,这种方法存在严重的局限性。
GRPO 的问题:奖励信号压缩
直接将 GRPO 应用于多奖励设置存在一个被忽视的问题:它会导致奖励信号的严重压缩,造成优势估计中的信息损失。
GRPO 的优势计算方式:
对于一个包含 G 个响应的组和 n 个奖励的任务,GRPO 首先计算每个响应的总奖励: rsum(i, j) = r1(i, j) + ⋯ + rn(i, j)
然后对总奖励进行分组归一化: $$A^{(i,j)}_{\text{sum}} = \frac{r_{\text{sum}}^{(i,j)} - \mathrm{mean}\{ r_{\text{sum}}^{(i,1)}, \ldots, r_{\text{sum}}^{(i,G)}\}}{\mathrm{std}\{ r_{\text{sum}}^{(i,1)}, \ldots, r_{\text{sum}}^{(i,G)} \}}$$
问题示例:
考虑一个包含 2 个二值奖励和 2 个响应的简单场景: - 总奖励组合可能有:(0,1)、(0,2)、(1,2) 等 - GRPO 会将这些不同的奖励组合映射到完全相同的优势值 (−0.7071, 0.7071) - 这意味着 (0,2) 和 (0,1) 会被视为具有相同的学习信号,尽管前者表示两个奖励都得到满足,而后者只满足一个
核心洞察
GDPO 的核心洞察是:每个奖励应该进行独立的分组归一化,然后再进行聚合。这样可以保留不同奖励组合之间的细微差异,提供更准确的优势估计。
🚀 GDPO 算法流程
分组奖励解耦归一化
GDPO 的主要创新是将奖励归一化过程解耦,对每个奖励进行独立的分组归一化,然后再求和并进行批处理归一化。
GDPO 的优势计算步骤:
每个奖励独立归一化: 对每个奖励 rk 进行分组归一化: $$A^{(i,j)}_k = \frac{r_k^{(i,j)} - \mathrm{mean}\{ r_k^{(i,1)}, \ldots, r_k^{(i,G)}\}}{\mathrm{std}\{ r_k^{(i,1)}, \ldots, r_k^{(i,G)}\}}$$
归一化优势求和: 将所有奖励的归一化优势相加: Asum(i, j) = A1(i, j) + ⋯ + An(i, j)
批处理归一化: 对总和进行批处理级别的归一化,确保数值范围的稳定性: $$\hat{A}^{(i,j)}_{\text{sum}} = \frac{A^{(i,j)}_{\text{sum}} - \mathrm{mean}\{A^{(i',j')}_{\text{sum}}\}}{\mathrm{std}\{A^{(i',j')}_{\text{sum}}\} + \epsilon}$$
优势估计改进
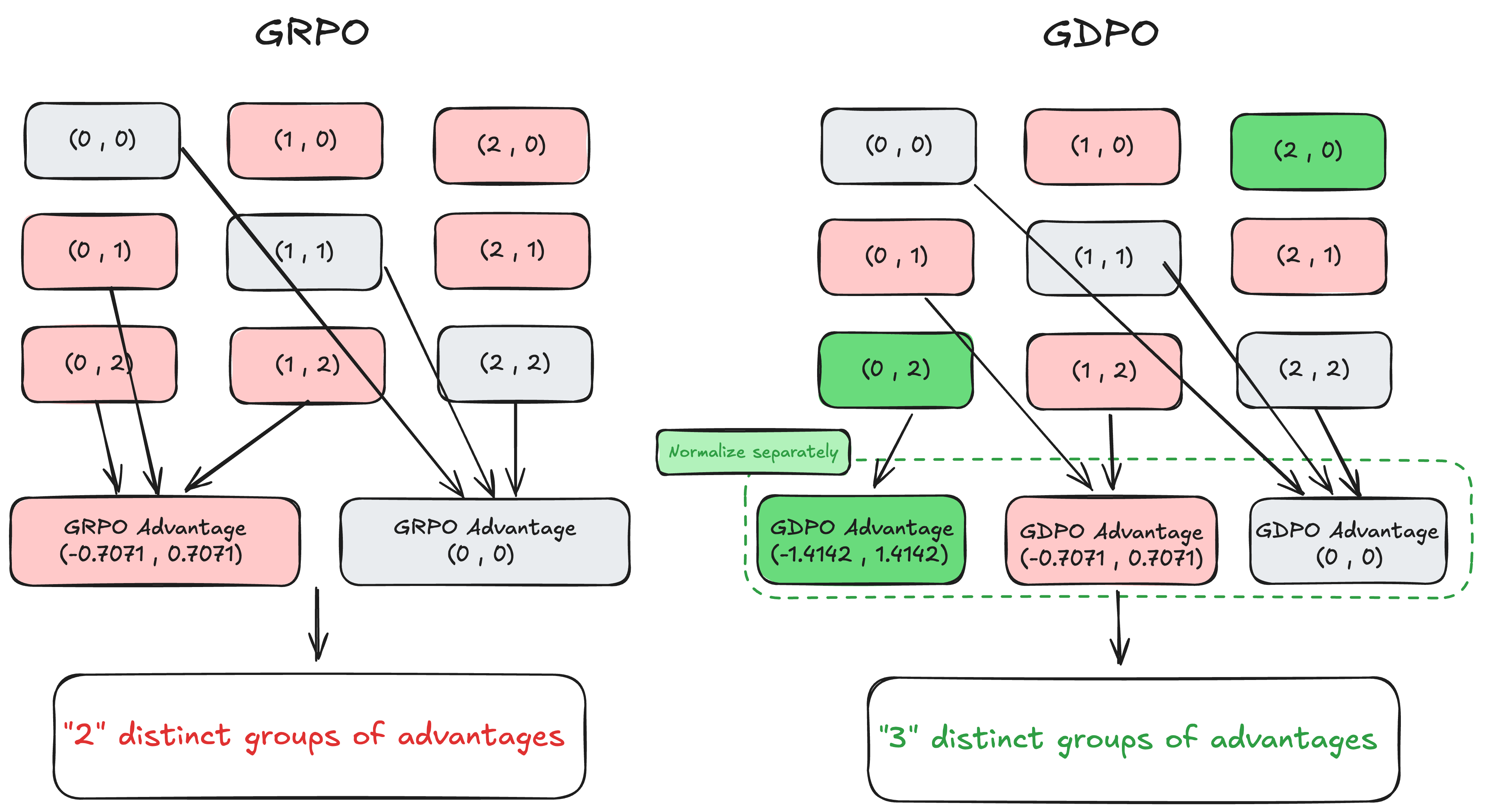
通过解耦归一化,GDPO 能够保留更多的优势差异。例如: - 在 2 个二值奖励和 2 个响应的场景中 - (0,1) 现在的优势值是 (−0.7071, 0.7071) - (0,2) 现在的优势值是 (−1.4142, 1.4142)
这更准确地反映了 (0,2) 应该产生更强的学习信号。
处理优先级差异
GDPO 还提供了有效处理奖励优先级差异的方法:
1. 奖励权重调整: 为每个奖励分配不同的权重: Asum(i, j) = w1A1(i, j) + ⋯ + wnAn(i, j)
2. 条件奖励设计: 对于难度差异较大的奖励,可以将简单奖励条件化到困难奖励上: $$r_k = \begin{cases} r_k, & \text{if } r_l \geq t \\ 0, & \text{otherwise.} \end{cases}$$
这种方法强制模型首先最大化优先级高的奖励。
🎯 实验结果
任务设置
研究团队在三个不同任务上比较了 GDPO 和 GRPO:
- 工具调用任务: 优化工具调用正确性和格式合规性两个奖励
- 数学推理任务: 优化准确性和长度约束两个奖励
- 代码推理任务: 优化代码生成准确性、长度约束和 bug 率三个奖励
主要结果
工具调用任务

GDPO 在平均准确率和格式正确性上均显著优于 GRPO。
数学推理任务
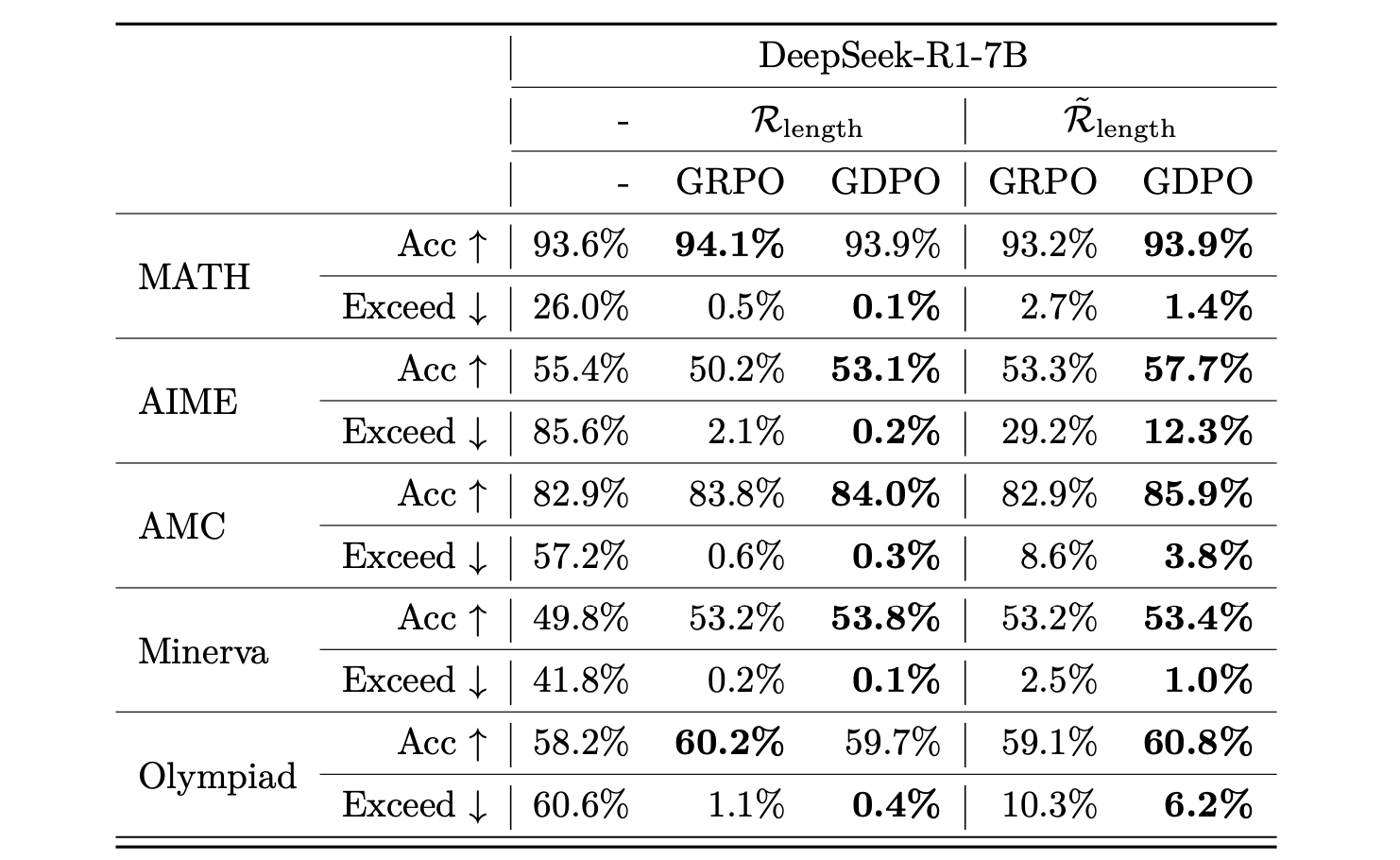
GDPO 不仅提高了准确性,还更好地控制了响应长度。
代码推理任务
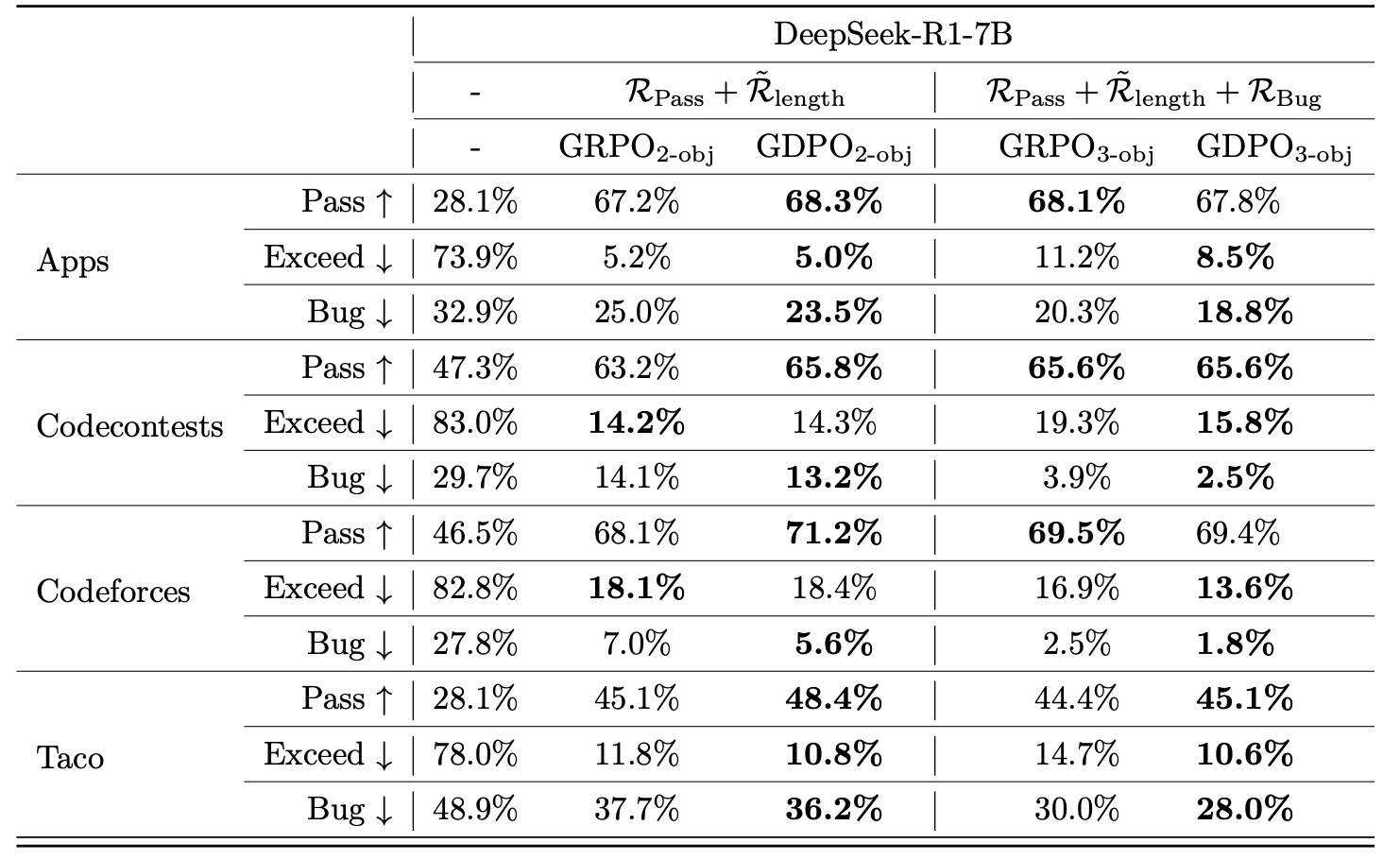
GDPO 在 2 目标和 3 目标优化中均优于 GRPO:在 3 目标优化中,GDPO 实现了 61.97% 的平均通过率,12.13% 的平均超限率,和 12.76% 的平均 bug 率
训练稳定性
GDPO 显示出比 GRPO 更稳定的训练曲线: - 在工具调用任务中,GDPO 持续收敛到更高的奖励值 - 在数学推理任务中,GDPO 消除了 GRPO 观察到的训练崩溃问题
💡 洞察与结论
关键观察
1. 解耦归一化的重要性: 每个奖励的独立归一化保留了奖励组合之间的细微差异,提供了更精确的优势估计。
2. 训练稳定性: 批处理级别的归一化确保了数值范围的稳定性,防止了训练过程中的梯度爆炸或消失问题。
3. 优先级处理: 条件奖励设计比简单的权重调整更有效地处理了难度差异大的奖励场景。
局限性与未来工作
尽管 GDPO 在多奖励优化中表现出色,但仍存在一些局限性: - 需要更多研究来确定最佳的批处理归一化策略 - 在处理大量奖励(如 10 个或更多)时的性能需要进一步评估 - 与其他多目标优化方法的比较研究
结论
GDPO 是一种简单而有效的多奖励强化学习优化方法,通过解耦奖励归一化过程,解决了 GRPO 存在的奖励信号压缩问题。实验结果表明,GDPO 在各种任务上均优于 GRPO,实现了更高的准确性和更好的训练稳定性。对于需要对齐语言模型与多样化人类偏好的应用场景,GDPO 提供了一个强大的优化框架。
参考文献
[1]GDPO 论文:GDPO: Group reward-Decoupled Normalization Policy Optimization for Multi-reward RL Optimization
[2]代码实现:GitHub - NVlabs/GDPO